cubic_spline Class Reference

#include <cubic_spline.h>

Collaboration diagram for cubic_spline:

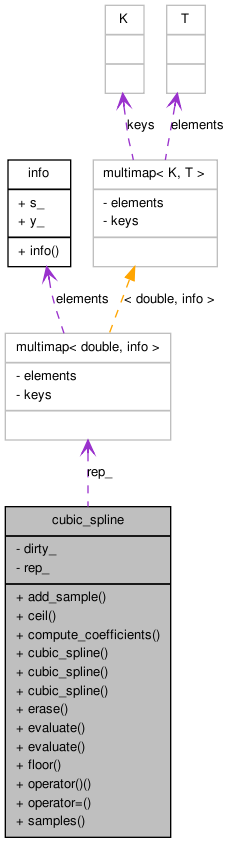
Classes
struct	info
	info stored for each x value in the sample data set More...
Public Types
typedef rep_t::const_iterator	const_iterator
	const iterator
typedef rep_t::iterator	iterator
	mutable iterator
typedef std::multimap< double, info >	rep_t
	sorted list of data pts
typedef rep_t::value_type	value_t
	aids in inserting data
Public Member Functions
void	add_sample (double x, double y)
	Add a new data point to the sample and store it its proper sorted order.
const_iterator	ceil (double const &x) const
	get an iterator to the sample whose X is immediately above 'x'. Returns end() if no such sample exists. O(ln(N)) performance
void	compute_coefficients ()
	compute s_'s.
template<class InputIterator >
	cubic_spline (InputIterator first, InputIterator last)
	cubic_spline (cubic_spline const &rhs)
	Copy constructor.
	cubic_spline ()
	Default constructor.
void	erase ()
	Eliminates all data points.
double	evaluate (double) const
	evaluate 1 point
template<class OutputIterator >
void	evaluate (double start_x, double delta_x, OutputIterator begin, OutputIterator end)
	Create a collection of interpolated values. Output those values through an iterator that points to a pair<X,Y> where X, and Y are assignment compatible with double. The begin,end variables define the standard output iterator range logic. The first value output will be (start_x, f(start_x)), the second will be (start_x+delta_x, f(start_x+delta_x)), and so forth.
const_iterator	floor (double const x) const
	get iterator to the sample whose X is less than or equal to x and which is higher than any other sample. O(ln(N)) performance
double	operator() (double x) const
	Evaluate the spline at location x.
cubic_spline &	operator= (cubic_spline const &rhs)
	Assignment operator.
rep_t const &	samples () const
	Get a list of the actual sample data.
Private Attributes
bool	dirty_
rep_t	rep_

Detailed Description

Create the spline by copying, constructing, assigning etc. Once you have all the data points added (as above or using add_sample), you can use the function call operator to evaluate the spline at any X value. For example:

cubic_spline s;

s.add_sample(0,0); // basically sinusoidal wave form s.add_sample(1,1); s.add_sample(2,0); s.add_sample(3,-1); s.add_sample(4,0);

double value = s(1.5); // about .5

You can iterate over the actual sample data using the samples() method. You can interpolate multiple points using:

evaluate(1.0,.2, begin_output, end_output);

see below.

Note that once the coefficients have been calculated, you can look at the sample data to get the

Definition at line 44 of file cubic_spline.h.

Member Typedef Documentation

typedef rep_t::const_iterator const_iterator

const iterator

Definition at line 92 of file cubic_spline.h.

typedef rep_t::iterator iterator

mutable iterator

Definition at line 91 of file cubic_spline.h.

typedef std::multimap<double,info> rep_t

sorted list of data pts

Definition at line 89 of file cubic_spline.h.

typedef rep_t::value_type value_t

aids in inserting data

Definition at line 90 of file cubic_spline.h.

Constructor & Destructor Documentation

cubic_spline ( )

Default constructor.

Definition at line 122 of file cubic_spline.h.

Here is the caller graph for this function:

cubic_spline ( cubic_spline const & rhs )

Copy constructor.

Definition at line 127 of file cubic_spline.h.

cubic_spline	(	InputIterator	first,
		InputIterator	last
	)

< construct from an iterator range. The input data must refer to pair<X,Y> where X and Y are assignment compatible with double.

Definition at line 141 of file cubic_spline.h.

Here is the call graph for this function:

Member Function Documentation

void add_sample	(	double	x,
		double	y
	)

Add a new data point to the sample and store it its proper sorted order.

Definition at line 94 of file cubic_spline.h.

Here is the caller graph for this function:

const_iterator ceil ( double const & x ) const

get an iterator to the sample whose X is immediately above 'x'. Returns end() if no such sample exists. O(ln(N)) performance

Definition at line 180 of file cubic_spline.h.

Here is the caller graph for this function:

void compute_coefficients ( )

compute s_'s.

Compute the second derivative of the interpolation functions and store them in the s_ member of the info associated with every x/y pair.

Definition at line 23 of file cubic_spline.cxx.

Here is the caller graph for this function:

void erase ( )

Eliminates all data points.

Definition at line 109 of file cubic_spline.h.

double evaluate ( double x ) const

evaluate 1 point

Definition at line 112 of file cubic_spline.cxx.

Here is the call graph for this function:

void evaluate	(	double	start_x,
		double	delta_x,
		OutputIterator	begin,
		OutputIterator	end
	)

Create a collection of interpolated values. Output those values through an iterator that points to a pair<X,Y> where X, and Y are assignment compatible with double. The begin,end variables define the standard output iterator range logic. The first value output will be (start_x, f(start_x)), the second will be (start_x+delta_x, f(start_x+delta_x)), and so forth.

Definition at line 156 of file cubic_spline.h.

Here is the caller graph for this function:

cubic_spline::const_iterator floor ( double const x ) const

get iterator to the sample whose X is less than or equal to x and which is higher than any other sample. O(ln(N)) performance

Returns the iterator to the sample whose X component is as high as possible but <= x. Returns end() if no such sample exists. Consider the sequence:

10, 11, 12

If you ask for 9, you will get end() returned. If you ask for 13, you will get an iterator to 12. If you ask for 11.5, you will get an iterator to 11.

Definition at line 177 of file cubic_spline.cxx.

Here is the caller graph for this function:

double operator() ( double x ) const

Evaluate the spline at location x.

Definition at line 116 of file cubic_spline.h.

Here is the call graph for this function:

cubic_spline& operator= ( cubic_spline const & rhs )

Assignment operator.

Definition at line 133 of file cubic_spline.h.

Here is the call graph for this function:

rep_t const& samples ( ) const

Get a list of the actual sample data.

Definition at line 119 of file cubic_spline.h.

Member Data Documentation

bool dirty_ [private]

Definition at line 202 of file cubic_spline.h.

rep_t rep_ [private]

Definition at line 201 of file cubic_spline.h.

The documentation for this class was generated from the following files:

include/cxxtls/cubic_spline.h
lib/cubic_spline.cxx

cubic_spline Class Reference

Classes

Public Types

Public Member Functions

Private Attributes

Detailed Description

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation